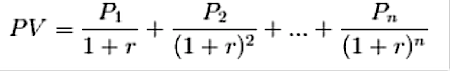The incessant noise around whether to taper or not to taper got me thinking that it may be a good idea to cover off on some bonds investing 101. Afterall, there is a bit more to investing in bonds than just price and yield.
Additionally, Korey Bauer has written a couple of great articles on bonds: Why Bond Yields May Be Headed Lower (Short Term) and Why Bond Yields May Continue to Fall.
In the example below, I have carried out the calculations in full. Of course they can be done in Excel, Tables, or by other means but there is something rewarding in the long-hand version of the calculations. As a reminder of the formula, it is:
Bonds Calculation Table
Figure 1: www.financeformulas.net
My calculations are in Figure 2 and to show the impact of the discount factor each year I have used ((1/ (1+y)n)), multiplied by the coupon, resulting in a slight variation on the formula above. The final year also includes the par value of the bond, multiplied by the discount factor for that year, to give the total value of capital and interest over the period.
Part of the rationale for this article was also to show that investors should not take flight at yield increases. As we know, the bond price is inversely proportional to the yield, so an upward move in yields signals a reduction in bond price. Selling at this point may realise a capital loss, although the temptation to purchase bonds with a shorter maturity may seem compelling as they will be less sensitive to variations in yield.
Behavioural finance also has an impact here, as investors are much more sensitive to sustaining losses than they are to making gains. Therefore, a principal loss may be hard for some to countenance. To this we can also add mental accounting and myopic loss aversion, all elegantly explained by Kahneman.
In the example, the investor buys a bond on October 1st 2013, and it has seven years to maturity. It has a par value of $100, a coupon of 2% and the current yield is 1.95%. The investor pays $102.06.
As we can see, one year later the yield has risen by 95 basis points, resulting in a principal loss of $6.95. After another year, on 1st October 2015, yields have risen by a further 60 basis points and the principal loss for the year is $8.83. On the third anniversary, yields have increased again, this time by 50 basis points. This results in loss on the principal of $6.64 for that year. These changes can be seen in Figure 2:
Figure 2: My calculations
The interesting point to note is that we can see sensitivity to interest rate changes has fallen, slowing the rate of price decline. We also have to consider that the investor will have received coupon payments of $5 in each of these three years, and although the principal value has dropped by $6.64, there has been an income of $15 to offset this. The impact of selling in each year is evident and suggests that all other factors being unchanged, the investor should resist the urge to sell. This is easier said than done of course, especially with our inherent loss aversion.
It is also important to note that this example does not consider the tax implications if the bonds were held in a mutual fund with the associated tax implications, rather it considers an individual investor using a brokerage account.
References:
- Kahneman, D. (2011) Thinking, fast and slow Allen Lane Penguin Group London
Twitter: @MillarAllan @seeitmarket
Any opinions expressed herein are solely those of the author and do not in any way represent the views or opinions of any other person or entity.